Complex formulas in Survey123 – empower your users

Survey123 has turned out to be an invaluable tool for data collection within the ArcGIS ecosystem. Survey123 covers use cases from collecting simple data via online forms to supporting complex inspections in a disconnected environment. Recently we helped out a client with some complex formulas in Survey123, and I thought it would be a wonderful excuse to talk about the power of calculations in Survey123. This post contains some math and assumes that you already know how to edit a form using Excel and Survey123 Connect with the XLSForm specification that Survey123 uses. You can find more in the documentation.

A few tips:

• I’m using the decimal type for demonstration here, but you can use calculation instead to hide the intermediate values
• The Survey123 Calculation language is a little hard to read, I suggest making multiple steps using the calculation type
• If you wanted to keep the intermediate steps, simply keep the decimal type and hide those fields

The Survey123 Expression Language

The language used in Survey123 (or the XLSForm specification that Survery123 uses) can be a little bit tough. The thing that gets most people right off the bat is the division operator. You can’t use /; you have to use div. I know, strange! That’s the strangest one though.

It does include things like pi() for π and some basic math functions. The part we need for this tutorial though is a floor function that doesn’t exist. Fortunately, the int function does effectively the same thing. It will always round down, so int(9.1) = int(9.9) = 9.

For the complete listing of math operators that can be used when creating complex formulas in Survey123, as well as some other useful ones like regular expressions see the XLSForm documentation.

Survey123 formulas: Distance -> Degrees

WARNING: MATH AHEAD!

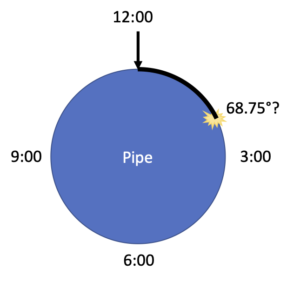
In our scenario, users were inspecting a buried pipeline (Survey123 is great for inspecting all kinds of assets, even things like buried water lines) and noting the position of a defect or problem on the line by measuring it using a tape measure from the top of the pipe:

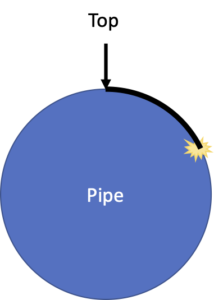
If you imagine that we cut the pipe in half and look at the open end of it, that’s the cross-section. In the image, you can see the location we want to measure and how we would measure its position from the top of the pipe.

So now we know two things:

• The distance to our defect (3 inches)
• The diameter of our pipe (5 inches) (our database already knows this because our GIS is fantastic)

Computers prefer to see things like this in degrees where 0 is the top of the pipe, 90 is to the right, 180 at the bottom, and 270 to the left:

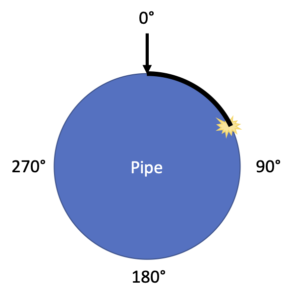
We can solve this with a simple proportion:

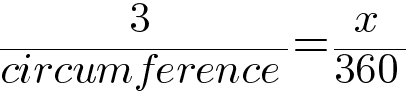
But how do we get the circumference? Fortunately, Archimedes¹ has us covered with the formula C = π * d. And we have d, it’s our diameter, so that gives us:

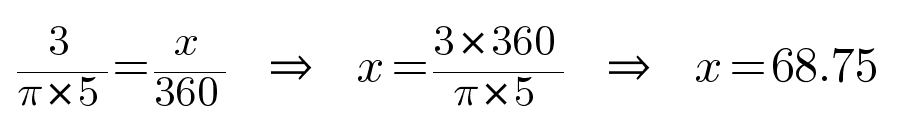
So, x is 68.75°. Doing a quick check, that looks right; it’s about 75% of the way around to our 90° mark.

Now we can write that using the Survey123 expression language like this:

360 * ${distance} div (pi() * ${diameter})

Survey123 formulas: Degrees-> Clock position

Degrees are great for computers, but they are kind of hard for humans to understand. Fortunately, that cross-section looks like something we are all familiar with: a clock. We need to calculate the hours and the minutes. Hours look like another ratio problem…

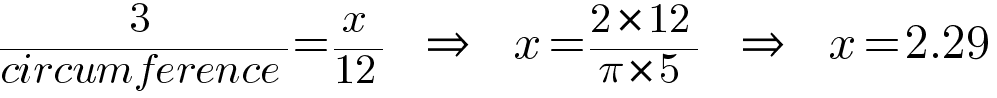
So, x is 2.29, a little after 2:00 on our pipe. Looks good! We can translate that into Survey123 expression language like this:

12 * ${distance} div (pi() * ${diameter})

But how do we get the minutes? Well, we know there are 60 minutes in an hour so:
0.29 * 60 = 17.4 which gives us 2:17

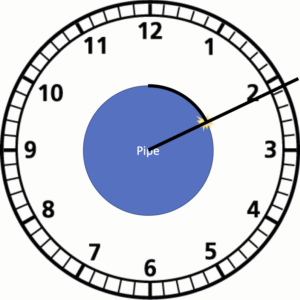
Remember: we are only looking at the hour hand here, so it’s the hour hand at 2:00 + 17 minutes.
To get this in Survey123 we can simply subtract the floor() of the number:

2.29 - floor(2.29) = 2.29 - 2 = 0.29
Hours = floor((3*12) / (π*5))
Minutes = ((3*12) / (π*5) - Hours ) * 60

Unfortunately, there is no floor() function in the Survey123 expression language. But we do have int(). It turns out that int behaves the same way as floor (see notes above), so we can build our complex Survey123 formulas like this:

decimal_hours = 12 * ${distance} div (pi() * ${diameter})
floor_hours = int(${decimal_hours})
decimal_minutes = (${decimal_hours} - ${floor_hours}) *60
clock_position = string(${floor_hours}) + ":" + string(round(${decimal_minutes},0))

I snuck in one final round() to trim the decimal places off of the minutes here which causes it to round to 18 minutes instead of 17.

Are you using Survey123 to its full potential?

We have helped so many customers over the years take their Survey123 forms to the next level that at this point we’re what you would call experts. If you want to save some time and money and make your users more productive with Survey123, talk to us!

1 – Archimedes didn’t understand π yet, but he did figure out the relationship between circumference and diameter by calculating the perimeters of inscribed regular polygons.

Clock Picture from http://www.clipartbest.com/clipart-RcdRrp7c9

XLSForm formula images built with https://math.tools/equation/image

All other art is my own.