Will AI Win March Madness at dymaptic?

"May the odds be ever in your favor," I declared as I prepared to unleash the artificial intelligence upon the unpredictable battlefield of brackets, where the only true certainty was the madness of March. – Chat GPT 

I don’t know much about basketball. I’m pretty sure it’s the one with the round ball where they can’t use their feet, though! Even though I don’t know much about basketball, I still like to participate in March Madness brackets with my friends, my family, and this year, my coworkers. But how can I turn something that I don’t know much about into something that I enjoy? 

I add something that I do know about: Machine Learning! 

Disclaimer: This is not a rigorous model—it’s not even a good model. It might not even qualify as a “model.” It was done in about 2 hours the night before brackets were due. There was no peer review. But it was fun, and that was the point! 

I didn’t have much time to get this model trained and working, so I went very, very simple. I started with each team’s number of wins vs total games and called that their win percentage. 

I needed a proxy for how likely the win percentage is to predict the next win. For this, I looked at each team's last several years of wins and computed the variance in that data. If the variance is low, then whatever they are doing (winning or losing), they will keep doing it. If the variance is high…well, I think that’s what they call a “potential upset.” 

Next, I can look at each initial pairing in the first round of the tournament. Let's say we have Team A and Team B for each pair. For each team, we take their win percentage and multiply it with the variance. From there, I compute the probability that Team A will beat Team B, build a standard distribution around that, and sample it to get the final probability that Team A will win. 

But Christopher!? How do you convert the number of wins (win percentage) into a probability you will win a game?

Good question! For that, we can look at how chess does an Elo Rating to compute the probability that Team A beats Team B as:

(a - ab) / a + b - 2 ab

Where: 

• a – The number of wins for Team A as a percentage (0-1) 
• b – The number of wins for Team B as a percentage (0-1) 

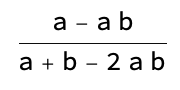
But that was not enough! I ran each game like that 100 times, doing a Monte Carlo simulation to see who was more likely to win. 

As usual in these kinds of projects, most of my time was spent cleaning and standardizing data. I found several datasets to use, but they all had different team names. Sometimes, I even found different team names within the same dataset for different years! So I spent a lot of time checking things out to ensure that, for example, these were all the same school: 

• Colorado State Rams 
• Colorado State 
• Colorado St. 

And so, without further ado, here are my picks for the Men’s bracket. 

After the first two rounds, I’m sitting in second place for the dymaptic pool, and I’m dead last in my friends-and-family pool (although with two slightly different brackets)! I’m in a three-way tie for first at dymaptic in in the Women’s tournament. It’s still anybody’s game for now! 

That’s what’s kind of fun about March Madness - it’s pretty unpredictable, and sometimes picking based on your favorite mascot is just as good as anything else!